Базовый уровень ЕГЭ по математике: полезные советы

Структура экзамена в 2025 году
- Количество заданий: 21 (все с кратким ответом).
- Время: 3 часа (180 минут).
- Максимальный балл: 21 (за каждое задание — 1 балл).
- Минимальный балл для аттестата: 7.
Типы заданий
- Арифметика и вычисления — дроби, проценты и округление.
- Алгебра — линейные и квадратные уравнения, неравенства.
- Геометрия — площади, углы, простейшие фигуры.
- Практические задачи — расчёты в бытовых ситуациях.
- Чтение графиков и таблиц — анализ данных.
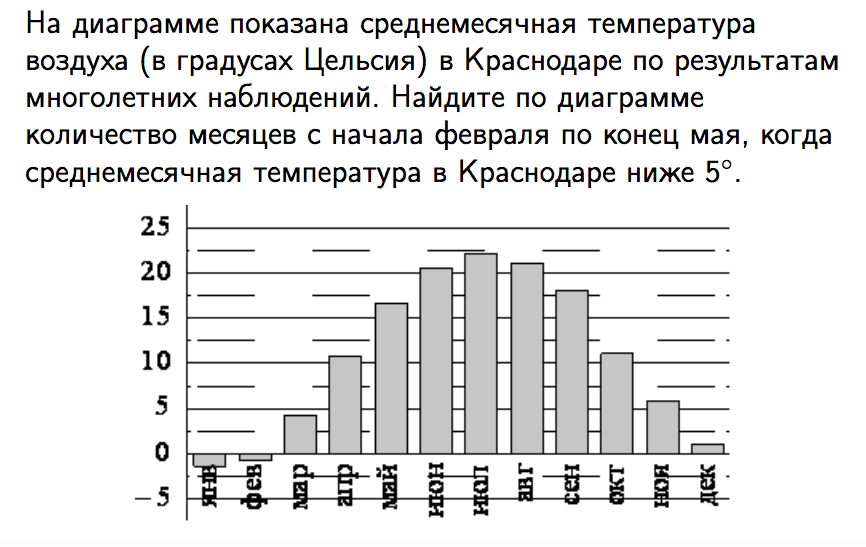
Типичный ответ
Очень часто школьники упускают из виду часть условия «с февраля по конец мая» и дают неправильный ответ на простейшую задачу — «Февраль, март, ноябрь, декабрь».
Хотя правильный ответ
«Февраль и март».
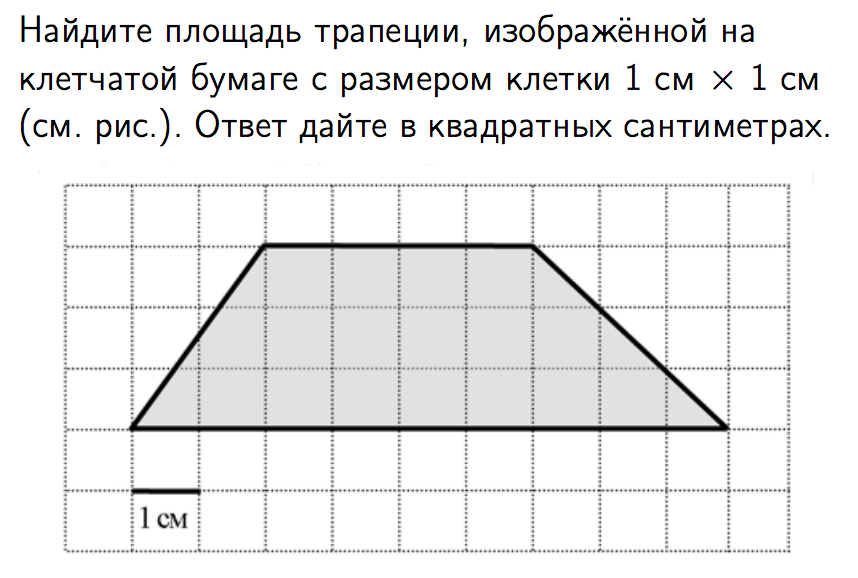
Способ 1. Делим трапецию на два треугольника по краям и прямоугольник в центре. Считаем площадь по клеточкам. Площадь прямоугольника – 12 см2.
Треугольники для удобства продолжаем до прямоугольников, считаем площадь этих прямоугольников (она получается 6 и 9 см2) и делим ее пополам. Таким образом, получается, что площадь первого треугольника – 3 см2, а второго – 4,5 см2. Складываем 3 + 12 + 4,5 и находим площадь трапеции = 19,5 см2.
Способ 2. Используем формулу для нахождения площади трапеции.
Где h — высота трапеции, a и b — основания.
S=123(9+4) = 19,5 см2.
Ответ сошёлся, значит он верный.

Чтобы решить эту задачу, нужно знать одну единственную формулу — Ньютона-Лейбница.
S=F(b) – F(а). Подставляем значения х в функцию, указанную в условии, находим F(–1) и F(–3), подставляем в формулу и получаем S=5–3=2.

Это одна из самых простых задач с точки зрения математики, хотя и стоит ближе к концу списка заданий. Здесь нужно всего лишь взять формулу, подставить в нее величины и правильно подсчитать.
Обращайте внимание на то, чтобы все упомянутые в задаче числа были указаны в одной системе измерений. При необходимости нужно перевести всё в одну систему, но в данном примере и этого не требуется.
m(t)=31,25
M(0)=250
T=3 мин
Вычисляем и получаем ответ: t=9.

Здесь тоже гораздо быстрее не делить с остатком, а прикинуть, сколько автобусов может понадобиться, а затем выполнить простую операцию умножения.
В этом случае нам надо перевести 274 человека, а в автобус влезает 46. Возьмем для начала цифру 6 и умножим на 46, получилось 276 человек. Это значит, что мы нашли правильный ответ, не углубляясь в сложные расчеты.

Для решения задачи часто нужно составить уравнение, а для этого важно не упустить ни одного элемента условия и правильно записать его математическим языком. Умение перевести текст задачи в уравнение — навык, который надо тренировать.
Вводим неизвестное: х — количество винограда. Чтобы составить уравнение, нам необходимо равенство. Что мы можем в данном случае уравнять? Сухое вещество, ведь оно остается одинаковым и в винограде, и в изюме. Если в винограде 82% воды, значит сухого вещества – 18%. Точно так же находим сухое вещество в изюме: 100 – 19 = 81%.
Получается, что 18% от неизвестного нам количество винограда – это то же самое, что 81% от 42 килограммов изюма. Составляем уравнение и решаем его:
х ∙ 18% = 42 ∙ 81%
Ответ: х = 189.
Как подготовиться
Шаг 1. Повторите основные темы
- Действия с дробями, процентами, степенями.
- Решение уравнений и неравенств.
- Основы геометрии — теорема Пифагора, площади фигур.
- Работа с графиками — линейными и квадратичными функциями.
Шаг 2. Решайте демоверсии и пробники
- Официальный сайт ФИПИ — актуальные варианты.
- Открытый банк заданий — похожие задачи на реальный экзамен.
- Тренировочные приложения.
Шаг 3. Научитесь правильно заполнять бланки
- Ответы записываются цифрами или десятичными дробями.
- Нельзя писать единицы измерения: например, «5 км» → просто «5».
Советы на экзамене
- Начните с лёгких заданий (1–15), потом переходите к сложным.
- Проверяйте арифметику — чаще всего ошибки в простых вычислениях.
- Не оставляйте пустых ответов — если не знаете, попробуйте угадать.
- Следите за временем — 180 минут хватит, но лучше не засиживаться.








